4 Problemas de valores en la frontera

Si, por ejemplo, $u(x, t)$ es una solución de una EDP, donde $x$ representa una dimensión espacial y $t$ representa el tiempo, entonces es posible prescribir el valor de $u$, o $\frac{\partial u}{\partial x}$, o una combinación lineal de $u$ y $\frac{\partial u}{\partial x}$ en un valor $x$ especificado, así como prescribir $u$ y $\frac{\partial u}{\partial t}$ en un instante dado $t$ (normalmente, $t=0$). En otras palabras, un problema de valores en la frontera puede consistir en una EDP, junto con condiciones de frontera y condiciones iniciales (Zill y Cullen 2008).

4.1 Ecuaciones clásicas

Aplicar el método de separación de variables para encontrar soluciones en forma de producto es muy común con las siguientes ecuaciones clásicas de la física matemática:

\[ k\frac{\partial^2 u}{\partial x^2} = \frac{\partial u}{\partial t}, \quad k > 0 \tag{4.1}\]

\[ \alpha^2 \frac{\partial^2 u}{\partial x^2} = \frac{\partial^2 u}{\partial t^2} \tag{4.2}\]

\[ \frac{\partial^2 u}{\partial x^2} + \frac{\partial^2 u}{\partial y^2} = 0 \tag{4.3}\]

o variantes ligeras de estas ecuaciones. Las EDPs 4.1, 4.2 y 4.3 se conocen, respectivamente, como la ecuación del calor unidimensional, la ecuación de onda unidimensional y la forma bidimensional de la ecuación de Laplace. El término “unidimensional” en el caso de las ecuaciones 4.1 y 4.2 se refiere al hecho de que $x$ denota una variable espacial, mientras que $t$ representa el tiempo; “bidimensional” en 4.3 significa que tanto $x$ como $y$ son variables espaciales. Si se compara 4.1-4.3 con la forma lineal en la Definición 3.1 (donde $t$ juega el papel del símbolo $y$), se observa que la ecuación del calor 4.1 es parabólica, la ecuación de onda 4.2 es hiperbólica y la ecuación de Laplace 4.3 es elíptica.

4.2 Condiciones iniciales

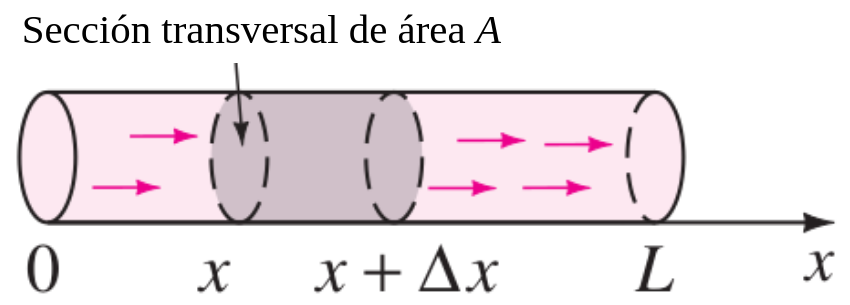
Dado que las soluciones de las ecuaciones 4.1 y 4.2 dependen del tiempo $t$, es posible especificar lo que ocurre en $t = 0$; es decir, establecer condiciones iniciales (CI). Si $f(x)$ representa la distribución inicial de temperatura en la varilla mostrada en la Figura 4.1 (a), entonces una solución $u(x, t)$ de 4.1 debe satisfacer la condición inicial única $u(x, 0) = f(x), \quad 0 < x < L$.

Por otro lado, para una cuerda vibrante podemos especificar tanto su desplazamiento inicial (o forma) $f(x)$ como su velocidad inicial $g(x)$. En términos matemáticos, buscamos una función $u(x, t)$ que satisfaga 4.2 y las dos condiciones iniciales: \[ u(x, 0) = f(x), \quad \left. \frac{\partial u}{\partial t} \right|_{t=0} = g(x), \quad 0 < x < L. \tag{4.4}\]

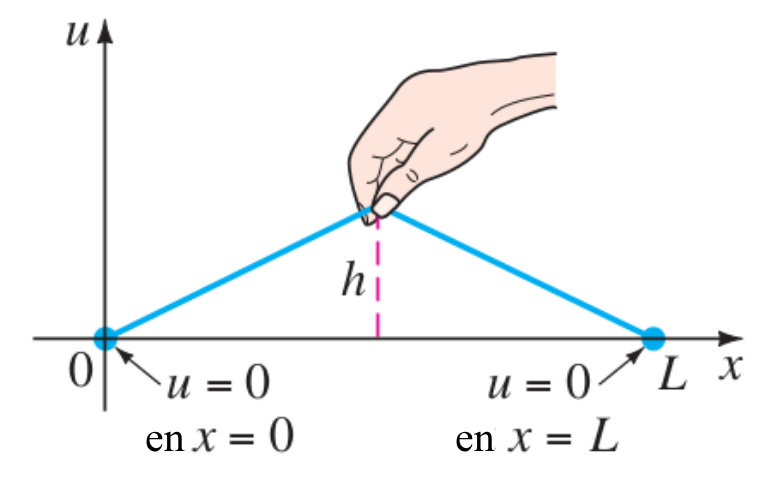
Por ejemplo, la cuerda podría ser tensada, como se muestra en la Figura 4.1 (b), o liberada desde el reposo $(g(x)=0)$.

4.3 Condiciones de frontera

La cuerda en la Figura 4.1 (b) está fija al eje $x$ en $x=0$ y $x=L$ para todos los tiempos. Ésto se interpreta a través de dos condiciones de frontera (CF): \[ u(0,t) = 0, \quad u(L,t)=0, \quad t>0. \] En éste contexto la función $f$ en la Ec 4.4 es continua y, en consecuencia, $f(0)=0$ y $f(L)=0$. En general, existen tres tipos de condiciones de frontera asociadas con las ecuaciones 4.1, 4.2 y 4.3. En la frontera es posible especificar los valores de una de las siguientes:

\[ \text{(i)}\quad u, \qquad \text{(ii)}\quad \dfrac{\partial u}{\partial n},\qquad \text{o}\qquad \text{(iii)}\quad \dfrac{\partial u}{\partial n} + hu,\quad \text{con $h$ constante.} \]

Aquí $\frac{\partial u}{\partial n}$ denota la derivada normal de $u$ (la derivada de $u$ en dirección perpendicular a la frontera). Una condición de frontera del primer tipo (i) es llamada condición de Dirichlet; una condición de frontera del segundo tipo (ii) es llamada condición de Neumann; y una condición de frontera del tercer tipo (iii) es conocida como condición de Robin. Por ejemplo, para $t>0$ una condición típica al extremo derecho de la varilla de la Figura 4.1 (a) puede ser:

\[\begin{align*} \text{(i)}' &\quad u(L,t) = u_0, \text{ con } u_0 \text{ constante} \\ \\ \text{(ii)}' &\quad \left. \dfrac{\partial u}{\partial x} \right|_{x=L} = 0 \\ \\ \text{(iii)}' &\quad \left. \dfrac{\partial u}{\partial x} \right|_{x=L} = -h(u(L,t)-u_m),\text{ con } h>0 \text{ y } u_m \text{ constantes} \end{align*}\]

La condición (i)’ simplemente establece que el límite $x=L$ se mantiene, por algún medio, a una temperatura constante $u_0$ durante todo el tiempo $t>0$. La condición (ii)’ indica que el contorno $x=L$ está aislado. Según la ley empírica de la transferencia de calor, el flujo de calor a través del borde (es decir, la cantidad de calor por unidad de área por unidad de tiempo conducida a través la frontera) es proporcional al valor de la derivada normal $\frac{\partial u}{\partial n}$ de la temperatura $u$. Por lo tanto, cuando el límite $x=L$ está aislado térmicamente, no fluye calor hacia dentro ni hacia fuera de la varilla, por lo que \[ \left. \dfrac{\partial u}{\partial x} \right|_{x=L} = 0. \]

Es posible interpretar (iii)’ como que el calor se pierde del extremo derecho de la varilla al estar en contacto con un medio, como el aire o el agua, que se mantiene a temperatura constante. Según la ley de enfriamiento de Newton, el flujo de calor hacia afuera de la varilla es proporcional a la diferencia entre la temperatura $u(L, t)$ en la frontera y la temperatura $u_m$ del medio circundante. Se observa que si se pierde calor por el extremo izquierdo de la varilla, la condición de contorno es \[ \left. \dfrac{\partial u}{\partial x} \right|_{x=0} = h(u(0,t)-u_m). \] El cambio de signo respecto de (iii)’ corresponde con el supuesto de que la varilla está a una temperatura más alta que el medio que rodea los extremos, de modo que $u(0, t) > u_m$ y $u(L, t) > u_m$. Para $x=0$ y $x=L$, las pendientes $u_x(0, t)$ y $u_x(L, t)$ deben ser positivas y negativas, respectivamente.

Por supuesto, en los extremos de la varilla se pueden especificar diferentes condiciones al mismo tiempo. Por ejemplo, podríamos tener \[ \left. \dfrac{\partial u}{\partial x} \right|_{x=0} =0 \quad \text{y} \qquad u(L,t)=u_0, \quad t>0. \]