5 Problemas de valor inicial
Las ecuaciones diferenciales son utilizadas para modelar problemas en ciencia e ingeniería que implican el cambio de una variable con respecto a otra. La mayoría de estos problemas requieren la solución de un problema de valor inicial, es decir, la solución de una ecuación diferencial que satisface una condición inicial dada.
En situaciones reales comunes, la ecuación diferencial que modela el problema es demasiado compleja para resolverse con exactitud, y se adopta uno de dos enfoques para aproximar la solución. El primer enfoque consiste en modificar el problema simplificando la ecuación diferencial a una que pueda resolverse con exactitud y luego utilizar la solución de la ecuación simplificada para aproximar la solución del problema original. El otro enfoque utiliza métodos para aproximar la solución del problema original. Este es el enfoque más común porque los métodos de aproximación proporcionan resultados más precisos e información de error realista (Burden y Faires 2010).
Para dar una idea más clara acerca de los problemas de valor inicial Burden y Faires (2010) brinda las siguientes definiciones y teoremas:
Definición 5.1 Se dice que una función \(f(t,y)\) satisface una Condición de Lipschitz en la variable \(y\) en un conjunto \(D \subset \mathbb{R}^2\) si existe una constante \(L>0\) tal que \[ |f(t,y_1) - f(t,y_2)| \leq L|y_1-y_2| \]
donde \(f(t,y_1) \ \ \text{y} \ \ f(t,y_2)\) están en \(D\). La constante \(L\) es llamada constante de Lipschitz para \(f\).
Definición 5.2 Se dice que un conjunto \(D \subset \mathbb{R}^2\) es convexo si para cualesquiera \(f(t,y_1), f(t,y_2) \in D\), entonces \(((1-\lambda)t_1 + \lambda t_2, (1-\lambda)y_1 + \lambda y_2)\) también pertenece a \(D\) para cada \(\lambda \in[0,1]\).
En términos geométricos, la Definición 5.2 establece que un conjunto es convexo siempre que, para cualesquiera dos puntos dentro del conjunto, todo el segmento recto entre ellos también pertenezca al conjunto Figura 5.1.
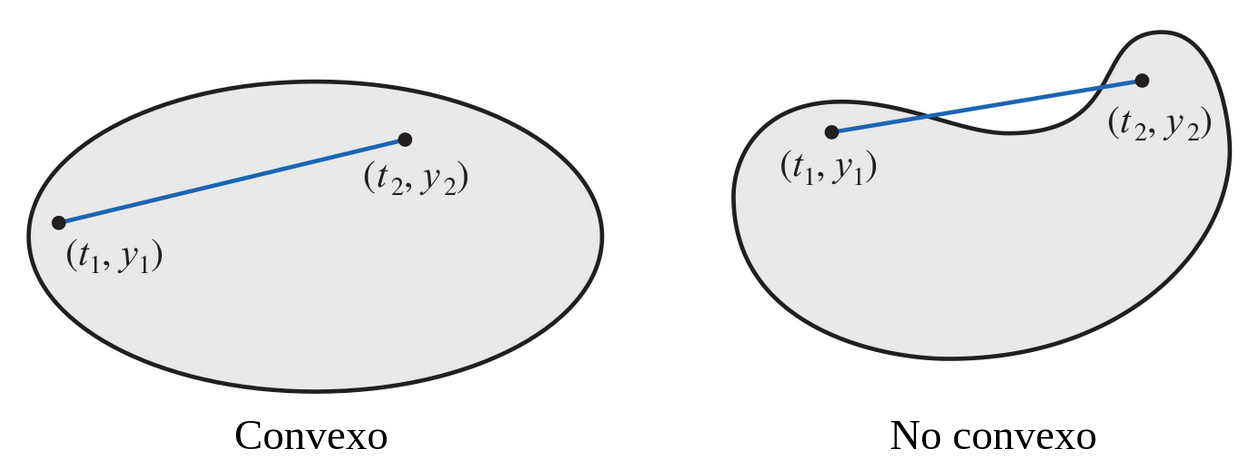
Teorema 5.1 Supongamos que \(f(t, y)\) está definida en un conjunto convexo \(D \in \mathbb{R}^2\). Si existe una constante \(L > 0\) con \[ \left|\dfrac{\partial f}{\partial y}(t,y) \right| \leq L, \quad \text{para todo} \ \ (t,y)\in D, \tag{5.1}\]
entonces \(f\) satisface una condición de Lipschitz en \(D\) en la variable \(y\) con una constante de Lipschitz \(L\).
Como se mostrará en el siguiente teorema, suele ser de gran interés determinar si la función involucrada en un problema de valor inicial satisface una condición de Lipschitz en su segunda variable, y la condición 5.1 suele ser más fácil de aplicar que la definición. Cabe destacar, sin embargo, que el Teorema 5.1 solo proporciona condiciones suficientes para que se cumpla una condición de Lipschitz.
Teorema 5.2 Supóngase que \(D = \{(t, y) | \ \ a \leq t \leq b, \ \ -\infty < y < \infty \}\) y que \(f (t, y)\) es continua en \(D\). Si \(f\) satisface una condición de Lipschitz en \(D\) en la variable \(y\), entonces el problema del valor inicial \[ y'(t)= f(t,y), \quad a\leq t \leq b, \quad y(a) = \alpha, \]
tiene una solución única \(y(t)\) para \(a\leq t \leq b\).
5.1 Problemas bien planteados
Ahora que hemos abordado, hasta cierto punto, la cuestión de cuándo los problemas de valor inicial tienen soluciones únicas, podemos pasar a la segunda consideración importante: cuándo aproximar la solución de un problema de valor inicial. Los problemas de valor inicial obtenidos mediante la observación de fenómenos físicos generalmente solo se aproximan a la situación real, por lo que necesitamos saber si pequeños cambios en el planteamiento del problema introducen cambios correspondientemente pequeños en la solución (Burden y Faires 2010).
A continuación se presentan otras definiciones así como teoremas que brindarán un conocimiento más sólido acerca de los problemas bien planteados. Se usará como referencia a Burden y Faires (2010).
Definición 5.3 Se dice que el problema de valor inicial \[ \dfrac{dy}{dt} = f(t,y), \quad a\leq t \leq b, \quad y(a) = \alpha, \tag{5.2}\] es un problema bien planteado si:
- Existe una única solución \(y(t)\) para el problema, y
- Existen constantes \(ε_0 > 0\) y \(k > 0\) tales que para cualquier \(\varepsilon\), con \(\varepsilon_0 > \varepsilon > 0\), siempre que \(δ(t)\) sea continua con \(|δ(t)| < \varepsilon\) para todo \(t\) en \([a, b]\), y cuando \(|δ_0| < \varepsilon\), el problema del valor inicial \[ \dfrac{dz}{dt} = f(t,z) + δ(t), \quad a\leq t \leq b, \quad z(a) = \alpha + δ_0 \tag{5.3}\] tenga una única solución \(z(t)\) que satisface: \[ |z(t)-y(t)| < k\varepsilon \quad \forall t \in[a,b], \]
donde \(k\) es conocida como constante de estabilidad.
El problema especificado por la Ecuación 5.3 se denomina problema perturbado asociado al problema original Ecuación 5.2. Se asume la posibilidad de que se introduzca un error en el planteamiento de la ecuación diferencial, así como la presencia de un error \(δ_0\) en la condición inicial.
Los métodos numéricos siempre se centrarán en la solución de un problema perturbado, ya que cualquier error de redondeo introducido en la representación perturba el problema original. A menos que el problema original esté bien planteado, hay pocas razones para esperar que la solución numérica de un problema perturbado se aproxime con precisión a la solución del problema original.
Teorema 5.3 Supongamos \(D = \{(t, y) | \ \ a \leq t \leq b, \ \ -\infty < y < \infty \}\). Si \(f\) es continua y satisface una condición de Lipschitz en la variable \(y\) en el conjunto \(D\), entonces el problema de valor inicial \[ \dfrac{dy}{dt} = f(t,y), \quad a\leq t \leq b, \quad y(a) = \alpha \] es bien planteado.
